Utilisation de l'algorithme DiamondSquare pour la génération de terrain
Date de publication : 19/04/2007 , Date de mise à jour : 19/0/2007
Par
Hiko Seijuro (Autres articles)
Ce tutoriel va expliquer comment l'algorithme DiamondSquare permet de générer des terrains aléatoires en 3D
1. Introduction
2. Explication de l'algorithme
2.1. Une petite explication
2.2. Un exemple
2.3. Prérequis
2.4. Phase du carré
2.5. Phase du diamant
2.6. hauteur pseudo aléatoire
3. Explication du code source
3.1. Architecture Générale
3.2. Explication de la classe CDiamondSquare
3.2.1. Interface
3.2.2. Mécanique interne
3.3. Code source
4. Capture d'écran
5. Conclusion
6. Remerciements
1. Introduction
L'algorithme DiamondSquare permet de générer des terrains de manière aléatoire. Il est relativement simple et ne
nécessite pas des heures d'étude pour le comprendre. La version vue est celle de base, on peut y ajouter
des améliorations comme l'insertion de détails lors de zoom, ...
Pour notre projet, nous allons utiliser le langage C++ et la bibliothèque OpenGL. Nous supposons cela acquis, du moins
les bases, car le projet ne nécessite pas de connaissances approfondies. L'Interface est développée sous QT4 et est
donc compatible Linux/Windows.
Le tutoriel va s'articuler autour de 2 parties : l'explication de l'algorithme en général puis l'explication de
l'implémentation en C++.
2. Explication de l'algorithme
2.1. Une petite explication
L'algorithme DiamondSquare, comme son nom l'indique, se base sur 2 phases : la phase du carré et la phase du diamant.
Il s'agit d'itérer ces 2 phases jusqu'à calculer tous les points de la matrice représentant le terrain 3D.
En effet, la largeur de la matrice représente les abscisses, la longueur les ordonnées et enfin chaque "case" de la matrice
représente la hauteur relative du point dont on vient de décrire les 3 composantes pour le situer dans un repère :
pour accéder à une case de la matrice on fait tab[x][y] = z; ce qui indique que les 3 coordonnées sont présentes.
Pour mieux comprendre le fonctionnement, je propose d'étudier un exemple.
2.2. Un exemple
Prenons un exemple simple pour expliquer l'algorithme. Soit une matrice 5X5 :
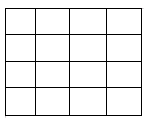
La phase du carré consiste à élever le centre du carré d'une valeur aléatoire (le point en rouge) :
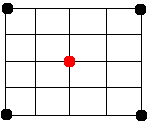
La phase du diamant consiste à élever le centre de chaque losange formé par le centre et les coins du carré précédent
d'une valeur aléatoire (les points en bleu). On peut constater déjà qu'on se retrouve confronté à un problème :
il n'y a pas quatre points complet pour former le diamant. Il faut donc tenir compte du cas particulier des bords :
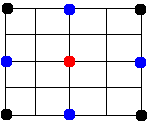
On réitère avec les carrés obtenus(vert),puis les diamants(orange) et ainsi de suite jusqu'à parcourir l'ensemble de la
matrice:
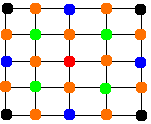
On obtient donc l'algorithme suivant :
espace = Largeur;
tant que espace > 1 faire
{
espace = espace / 2;
pour chaque carre de largeur espace faire
{
etape du carre;
}
pour chaque diamant de largeur espace faire
{
etape du diamant;
}
}
|
2.3. Prérequis
Comme vous pouvez le constater, il faut obligatoirement que la matrice ait pour largeur quelquechose du type 2^n+1, sinon
le calcul du centre serait faux, et l'algorithme ne marcherait pas.
En effet, on divise par 2 la largeur d'un carré ou d'un diamant à chaque étape ce qui explique le 2^n. De plus, on choisit le
centre et pour que ce centre soit déterminé, il faut que l'on ait le même écart à "gauche" et à "droite" du centre. Cela n'est
possible qu'avec une largeur impaire, d'où le 2^n+1.
2.4. Phase du carré
La phase du carré calcule la moyenne des 4 points formant le carré. Lors de cette phase, on est positionné sur le centre ayant
pour coordonnées (x, y). Sur un carré (a, b, c, d), on retrouve les coordonnées suivantes :
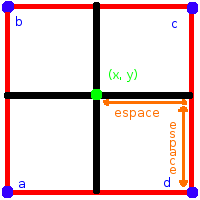
- a = (x-espace, y-espace)
- b = (x-espace, y+espace)
- c = (x+espace, y+espace)
- d = (x+espace, y-espace)
Mais il faut faire attention aux limites de la matrice. Il faut tester les coins du carré pour que leurs coordonnées soient
comprises entre 0 et largeurMatrice-1).
2.5. Phase du diamant
La phase du diamant calcule la moyenne des 4 points formant le losange (représentant le diamant). on est positionné sur le
centre qui a pour coordonnées : (x, y). Sur un diamant (a, b, c, d), on retrouve les coordonnées suivantes :
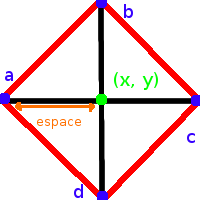
- a = (x-espace, y)
- b = (x, y+espace)
- c = (x+espace, y)
- d = (x, y-espace)
 |
Il faut encore faire attention aux limites de la matrice !
|
2.6. hauteur pseudo aléatoire
Comme le terrain est aléatoire, la hauteur d'un point doit être choisit au hasard. Néanmoins, pour ne pas avoir n'importe quoi,
il faut quand même contrôler sa valeur. On parle alors de hauteur pseudo aléatoire car cela n'est pas totalement dû au hasard.
Tout d'abord, la hauteur d'un point est calculée en fonction de la moyenne de la hauteur des points que l'algorithme a utilisé
pour l'obtenir.
On y ajoute une valeur aléatoire (supposée pure), à laquelle on applique un coefficient de lissage pour ne pas
avoir un terrain en dents de scie. De plus, on multiplie à cette valeur alétoire pure, l'espace entre le point cible et les
points sources, afin de garder la cohérence du terrain. Voici donc la formule pour obtenir la hauteur :
hauteur = moyenne() + random() * espace * lissage
|
Le coefficient de lissage est fractionnaire et donc inférieur à 1. Plus la valeur est élevée, moins le terrain sera lisse :
Lissage à 0.1
Lissage à 0.5
Lissage à 0.9
3. Explication du code source
3.1. Architecture Générale
Le but de l'application est d'interfacer la classe générant le terrain avec une interface. L'interface est faite en QT.
Voici la liste des classes :
-
CDiamondSquare : classe effectuant la génération du terrain
-
DiamondSquareWidget : classe représentant le composant effectuant l'affichage du terrain. Elle hérite de QGLWidget
- DiamondSquareApp : classe héritant de Ui::MyDialog qui représente l'interface
3.2. Explication de la classe CDiamondSquare
3.2.1. Interface
L'utilisateur ne dispose que du constructeur, de la génération, du changement de mode et de la méthode effectuant
l'affichage du terrain. L'objectif de cette organisation est de ne pas compliquer l'utilisation de la classe.
L'ordre d'utilisation de la classe est imposé :
- Appel du constructeur
- Appel de la méthode Generate
- Appel de la méthode Draw
La méthode ChangeMode est appelée pour permettre de passer du mode filaire au mode rempli et vice-versa.
3.2.2. Mécanique interne
Nous allons expliquer la méthode Generate plus en détails. Elle fait appel à 5 méthodes qui sont cachées à
l'utilisateur :
- Randomize qui génère un nombre aléatoire
- SquareStep qui effectue le calcul de la moyenne pour la phase du carré
- DiamondStep qui effectue le calcul de la moyenne pour la phase du diamant
- Init qui reserve la mémoire pour la matrice représentant le terrain
- SetColor qui applique la couleur en se basant sur la hauteur du point
Voici la partie importante de la méthode qui correspond à à l'algorithme général vu précédemment:
unsigned int unSpacing = m_unSize - 1;
while (unSpacing > 1)
{
int unHalfSpacing = unSpacing / 2;
for (unsigned int unI = unHalfSpacing; unI < m_unSize; unI += unSpacing)
{
for (unsigned int unJ = unHalfSpacing; unJ < m_unSize ; unJ += unSpacing )
{
m_vectPoints[unI][unJ] = SquareStep(unI, unJ, unHalfSpacing ) + Randomize() * unSpacing * m_fVariability;
}
}
for (unsigned int unI = 0; unI < m_unSize; unI += unHalfSpacing)
{
unsigned int unJStart = ((unI/unHalfSpacing) % 2 == 0 ) ? unHalfSpacing : 0;
for (unsigned int unJ = unJStart; unJ < m_unSize ; unJ += unSpacing )
{
m_vectPoints[unI][unJ] = DiamondStep(unI, unJ, unHalfSpacing ) + Randomize() * unSpacing * m_fVariability;
}
}
unSpacing = unHalfSpacing;
}
|
3.3. Code source
Le code source disponible est compilé sous linux avec QT en version 4.3. QT étant multiplateforme, il est possible de
compiler le code sous Windows mais je n'ai pas modifié le makefile en conséquence.
J'ai ajouté le doxyfile permettant de générer la documentation "doxygen" de la classe CDiamondSquare.
Pour compiler le code source, il faut se positionner dans le répertoire
DiamondSquareIHM, exécuter la commande
qmake puis la commande
make. L'executable sera le fichier DiamonSquareIHM obtenu.
Source
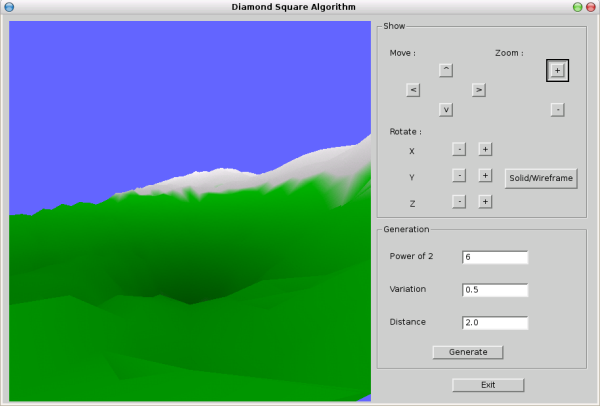
4. Capture d'écran
Voici une capture d'écran de l'IHM obtenu au lancé, avec les paramètres par défaut :
5. Conclusion
En conclusion, l'algorithme DiamondSquare n'est pas très difficile à mettre en oeuvre mais il faut etre un minimum rigoureux car
des erreurs d'étourderies sont vites arrivées.
Il est évident que des améliorations peuvent être apportées en jouant sur les détails et les calculs. Par exemple, si une zone est
affichée, on ne calcule que cette zone, ... Mais cela, je vous laisse le découvrir par vous même. Bonne prog !
6. Remerciements
Je tiens à remercier FearYourSelf, Laurent Gomila, Nico-Pyright, Farscape et mon professeur de
mathématique qui m'a fait découvrir cet algorithme : Adib Rahmouni.
Les sources présentées sur cette page sont libres de droits,
et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation
constitue une oeuvre intellectuelle protégée par les droits d'auteurs. Copyright ©
2007 Hiko-seijuro. Aucune reproduction,
même partielle, ne peut être faite de ce site et de l'ensemble de son contenu :
textes, documents, images, etc sans l'autorisation expresse de l'auteur.
Sinon vous encourez selon la loi jusqu'à 3 ans de prison et jusqu'à 300 000 E
de dommages et intérêts.
Cette page est déposée à la
SACD.
